Should you sell 1x1 options spreads or 1x2 ratio spreads to most quickly compound your short volatility portfolio?
We’ll explore this question by simulating the performance of portfolios from these two strategies under different market conditions. By the end of this post, you’ll hopefully have a deeper understanding of how long ratio spreads compound money more effectively.
Overview of the Strategies
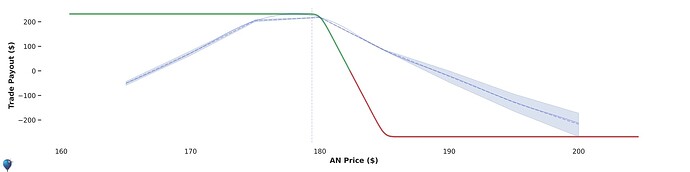
1. Traditional 1x1 Spread
- Structure: Sell one at-the-money (ATM) option and buy one out-of-the-money (OTM) option.
- Objective: Generate premium income while limiting potential losses.
- Risk Profile:
- Limited Profit: The maximum profit is capped at the premium received.
- Defined Risk: Potential losses are limited due to the protective OTM option. Higher odds of profit per trade than ratio spreads.
2. 1x2 Ratio Spread
- Structure: Sell one ATM option and buy two OTM options.
- Objective: Enhance profit potential and provide additional protection in extreme market moves.
- Risk Profile:
- Higher Upside Potential: Possibility for greater profits if the market moves favorably (long tail convexity).
- Less Premium Received: Potential for larger losses due to the $ needed to buy the extra long option. Lower odds of profit per trade than traditional spreads.
Options Portfolio Simulations
To evaluate which trade structure compounds a portfolio faster, we take 10,000 different portfolios, each starting with $100k that risk 2% of their total account value on a new trade every day for 1 year. Each trade has a duration of 10 days and trades are held till expiration. Short options were set to 50 delta (ATM) and long options were set to 10 delta (OTM). In every analysis, prices are perfectly efficient, meaning the volatility used for the underlying price and the volatility for the options prices are the same.
In all of these analysis, the options prices had perfect knowledge of the volatility of the underlying prices. Black-scholes was used for pricing options (with 0 interest rates).
We will look at the distributions of terminal wealth for each strategy to help us holistically compare the results of the portfolios’ ability to consistently compound returns.
Portfolio Performance Analysis
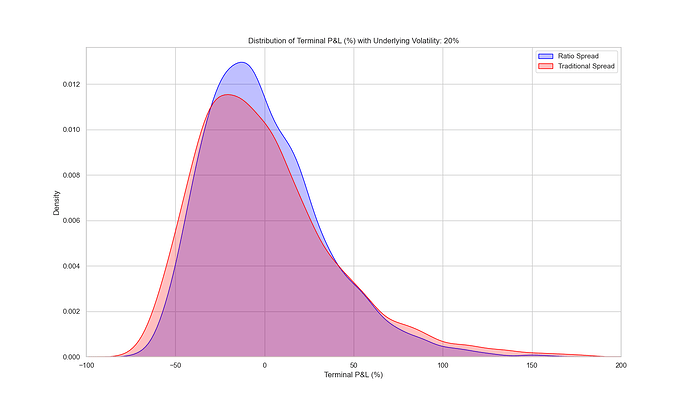
1. Normal Market Conditions
Characteristics:
- Normal Returns: Price movements follow a normal distribution with 20% annual volatility.
- Zero Autocorrelation: No predictable patterns; each price change is independent.
Results:
- Traditional Spread (Red):
- Fatter Left Tail: Of all the worst performing portfolios (bad luck), most of them were traditional spreads.
- Fatter Right Tail: Of all the best performing portfolios (good luck), most of them were traditional spreads.
- Ratio Spread (Blue):
- Tighter Distribution: More portfolios closer to 0% return, so less variance in terminal P/L.
- More Small Losses/Gains: More portfolios with small losses + small wins than traditional spreads.
Conclusion:
In normal markets, the ratio spread offers a chance to move some probability mass to the right at the expense of a smaller right tail. This makes the ratio spread more robust to losses and a have less volatility drag.
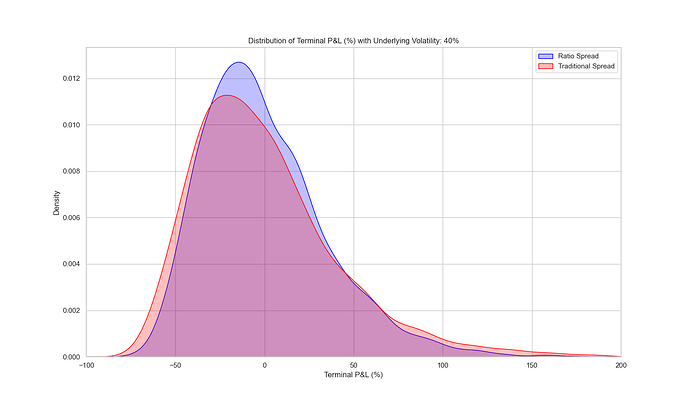
2. High Volatility
Characteristics:
- Increased Fluctuations: Prices move more dramatically at 40% annual volatility.
- Uncertainty: Higher risk of large market swings.
Results:
Conclusion:
Interestingly, this graph looks almost identical to the graph with 20% volatility. This is because the option pricing model used the same volatility as the underlying price distribution. Intuitively, since the options prices “knew” about the higher level of volatility, they were priced accordingly and the result P/L distribution is basically unchanged.
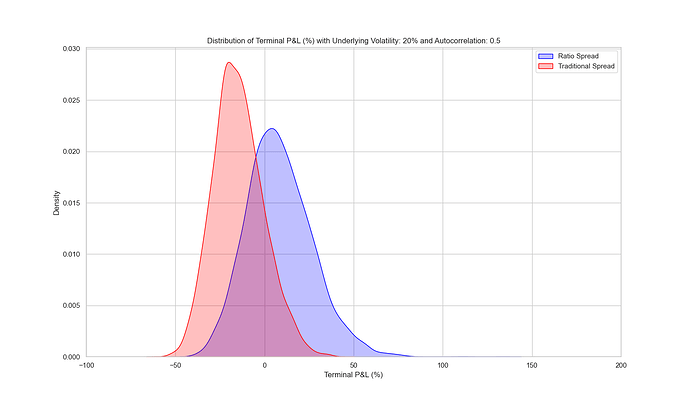
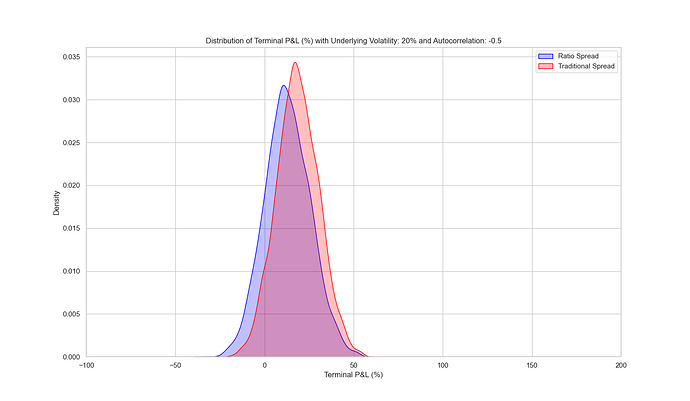
3. Autocorrelation
Characteristics:
- Trending Markets: Positive autocorrelation means past price movements have a positive relationship on future prices.
- Mean Reversion: Negative autocorrelation means past prices have a negative relationship on future prices.
In both cases, options prices reflected the level of volatility (20%) but not the autocorrelation of underlying prices.
Results:
Positive Autocorrelation (Trending)
In trending markets, the ratio spread significantly outperforms traditional spreads, due to the extra long option providing profit when the inevitable losing streak comes and traditional spreads keep bringing in back-to-back max losses.
Negative Autocorrelation (Mean-Reverting)
In mean-reverting markets, the traditional spread slightly outperforms the ratio spread because each trade collects a bigger credit, and the ratio spread’s extra long option is less useful.
Conclusion:
If we assume that we never know whether the price action will be trending/mean-reverting/random, then ratio spreads make the most sense. Ratio spreads slightly underperformed in mean-reversion conditions, but significantly outperformed in trending markets.
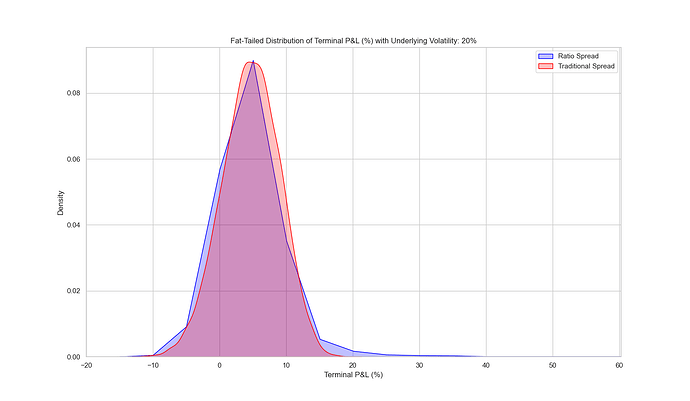
4. Fat-Tailed Returns
Characteristics:
- Extreme Events: Higher likelihood of significant market moves (both positive and negative).
- Non-Normal Distribution: Returns deviate from the normal distribution, increasing the risk of outliers (Student’s t-distribution).
Results:
- Traditional Spread (Red):
- More Small Wins: More mass over small wins (more consistent).
- Ratio Spread (Blue):
- Resilience: Additional OTM option provides better protection against extreme moves and results in a fat right tail (infrequent, big $ wins). Interestingly, it has a slightly bigger left tail.
Conclusion:
In markets with fat-tailed returns, ratio spreads offer the opportunity for bigger wins (fat right tail) at the expense of more frequent small losses (left shoulder of blue distribution). Fat tails more realistically represent market returns, and under these conditions are when ratio spreads have the opportunity for big gains.
Comparative Summary
| Aspect | Traditional 1x1 Spread | 1x2 Ratio Spread |
|---|---|---|
| Profit Potential | Limited and capped | Higher with potential for significant gains |
| Risk Exposure | Lower risk per trade with higher odds of profit per trade | Higher max loss per position and lower odds of profit per trade |
| Complexity | Simple to implement | Slightly more complex due to additional options |
| Performance in Volatility | Stable but may miss opportunities | Can capitalize on volatility but with increased risk |
| Protection in Extremes | Limited protection in extreme events | Potential for big wins due to extra OTM option |
| Suitability for Compounding | Slower compounding but getting lucky results in more $ | Faster compounding and more consistent |
Risk Management Strategies
Regardless of the chosen strategy, effective risk management is crucial:
- Position Sizing: Limit the amount risked per trade to a small percentage of the portfolio.
- Diversification: Spread risk across different assets or strategies or tenors.
- Monitoring and Adjustments: Regularly review positions and adjust as necessary.
Final Thoughts
Since ratio spreads offer the potential for faster compounding (especially with fat-tailed returns), Helium uses mostly ratio spreads for our Short Volatility Trades. One potential confounder is that in reality, tail options tend to trade with more premium, meaning we might be underestimating how much we’re paying for the 10 delta optinos.
Note: All analysis were performed with call spreads, but due to the symmetry of the analysis, the results would be the same with put spreads. Options were selected by their delta (based on the underlying distribution) from a flat volatility across all strikes.
Disclaimer: Options trading involves significant risk and is not suitable for all investors. The information provided is for educational purposes and should not be considered financial advice. Always conduct thorough research and consult with a professional before making investment decisions.