How to become a more accurate, holistic thinker by adding noise to your beliefs and mental models.
In machine learning, regularization is a key strategy used to prevent over-fitting (over-indexing on the data used to train it). By reducing the model’s confidence in its training data, we can help it generalize better to unseen data. The algorithm is taught humility, in essence, to ensure it doesn’t get too overconfident about its understanding of the world from the limited examples it has seen.
Let’s try and connect the idea of regularization to the realm of epistemology: the study of knowledge. Just like computer models, with mental models our goal is calibrating epistemic humility.
By deepening the context of our assumptions and beliefs (our ‘priors’), we make ourselves more open to new interpretations, reducing the chance of ‘over-fitting’ to the particulars of our past experiences. The goal of “Epistemic Regularization” is to broaden the scope and generality of your reference classes.
From a bayesian perspective, we’re increasing the scope/size of our priors, which in turn reduces the probability of each prior.
But here’s where it gets interesting: we’ve missed a key ingredient from our machine learning recipe — noise. In ML, we often add noise to our training data or gradient as a means of regularization, encouraging it to consider unseen, but possible scenarios. This is a counter-intuitive trick, where we carefully introduce random imperfections to improve the generalizability of our model.
The human mind equivalent of regularization might look something like adding a noise function (as accurate as possible to the true underlying distribution of occurrences) to how we process information, thus putting all experience into a much greater context that more deeply represents our underlying reality.
But how can we reason about things that didn’t happen?
Since we currently have no way of interacting with parallel universes, we simply don’t know what didn’t happen. But that doesn’t stop us from modelling counterfactuals. Just like regular models try to infer what will happen, a generative noise model tries to infer all events that were possible but didn’t happen. Our world of events is a small peak into the infinite world of the possible.
Going from the possible to the probable
If regularization is just adding noise, what noise distribution should we add?
Some algorithms use a noise function that maximizes the entropy, such as the normal distribution (bell curve). This ensures that noise encompass a broad range of potential outcomes and a has a high information content. This suggests that for humans like us, we should seek to add counterfactual events that are maximally revealing.
But we can do better than a simple normal distribution, since not all noise is equally helpful at calibrating our models. Suppose we are walking through a park and see a dog. If we add noise that changes the dog to a penguin instead, it’s not clear how helpful this is…
Ideally, we add a noise function that perfectly represents the true, unknown, distribution of potential events? This is the same thing as our generative model in the first place! We can use our current models to estimate this new noise distribution.
Isn’t this just circular reasoning?
If we’re using our current model to generate the noise function which gets fed back into our model, are we really going anywhere productive?
Bootstrappping our way to to Regularization
If learning the true noise function to add to our model is the same thing as learning the original model, we can iteratively bootstrap our way to a good model + a good noise function. The uncertainty of the world that limits our model is the same uncertainty that limits our ideal noise function.
This is similar to expectation maximization.
Here’s a simple algorithm we could use:
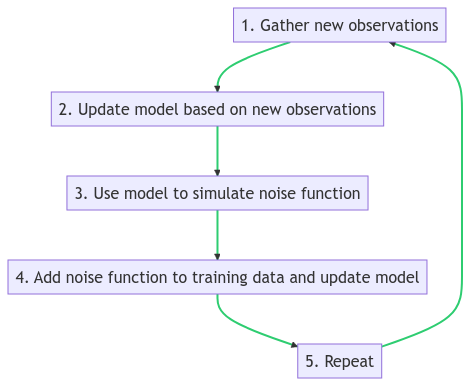
1.) Gather new observations
2.) Update model based on new observations
3.) Use model to simulate noise function
4.) Add noise function to training data and update model
5.) Repeat.
Okay so who cares, why is this useful?
Taking the serious effort to begin epistemically regularizing can improve the quality of your models and accuracy of your worldview.
How to epistemically regularize in your life:
-
Take counterfactuals seriously and build probabilities into your existing models for events that didn’t happen.
-
Increase the scope of possible outcomes when making a decision, even for outcomes with small probability that seem loco.
-
If a string of events had played out in a different but possible way, would this change your current thoughts, mental models and explanations? Are you overfitting to 1 particular thread of history instead of a more general, timeline-independent (multiverse) model of thinking?
-
Practice adding noise/random perturbations to your experience.
-
Lessen your reliance on fungible pieces of information. Like an interchangeable battery, fungible things can easily be swapped out for other things without having an effect on the outcomes we care about.
-
If you observe something, say a dog walking past you, don’t consider the observation in isolation but rather as a crude depiction of something much grander and more mysterious. What other types of dogs could you have plausibly seen? How does your reaction to this dog fit into all the possible interactions you could have with all possible pets?
Questions to Contemplate
In an alternate universe, there’s a version of you who grew up in a country on the other side of the globe. What kind of disagreements might you get in if you could have a conversation with your universal twin? What important things are you confident you would agree on?
Suppose you had been rejected from your current job/university/team/whatever. How does this change your self-perceptions of your ability/merit?
Adding this ‘noise’ to our mental ‘training data’ (epistemic regularization) pushes us to consider possibilities we haven’t encountered and prepares us for surprises that may lurk around the corner of the unknown future. It might feel uncomfortable and arbitrary at times, but remember, it’s this very discomfort of upsetting our current beliefs that keeps our cognitive engines in top shape, ready to face the uncertainties of life.
Let’s be clear here, though. Epistemic regularization doesn’t imply surrendering to chronic doubt or wallowing in a whirlpool of indecisiveness where everything is equally probable. Instead, it nudges us towards probabilistic maturity. It’s about the wisdom in understanding the vastness of what we don’t know, the courage to face uncertainty head-on, and the willingness to adapt and grow.
So, let’s learn to befriend uncertainty, to revel in the delightful symphony of ‘noise’ by embracing the power of not-knowing.